Il matematico polacco Benoît Mandelbrot (1924-2010) diede per la prima volta nel 1975 una definizione della figura frattale: dall’aggettivo latino fractus, interrotto o irregolare, “frattale” designa un insieme di figure descrivibili dall’esterno ricorrendo a un insieme di proprietà geometrico-matematiche.
La figura frattale è internamente omotetica, le parti assomigliano al tutto. La sua dimensione non è necessariamente intera: un punto in geometria euclidea è di dimensione pari a 0, una linea pari a 1, una superficie pari a 2 e così via. La dimensione frattale può essere un numero frazionario, un numero irrazionale…
È frattale il cavolo romano, è frattale la curva di Koch (Fig. 1),[1] è frattale il gomitolo di lana, a “metà strada” tra la dimensione euclidea di una linea mono dimensionale (la corda di lana) e la dimensione euclidea di un volume (la sfera del gomitolo).[2]
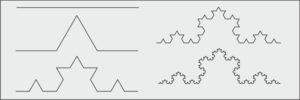
Fig.1
———-
Quando nasce il concetto di frattale?
Due acerrimi critici della sociologia della scienza come Alan Sokal e Jean Bricmont non hanno avuto dubbi: la frattalità fa parte del dominio delle matematiche. Di conseguenza, se le discipline umanistiche se ne sono appropriate ne hanno perpetrato un “reiterato abuso”.[3]
Teniamoci però a debita distanza: il padre dei frattali – al tempo – si definì “un vagabondo della scienza”.[4] Forse, il 1975 rappresenta una data troppo recente per poterci orientare. Mandelbrot rispose innanzitutto ad un’insufficienza della geometria, fino ad allora “troppo regolare e troppo fredda” per descrivere le insenature di una costa,[5] o i profili plastici e multiformi di una nuvola.[6]
Dove inizia questo vagabondaggio?
È il matematico polacco stesso a chiamare direttamente in causa un passato recondito.
In una lettera del 1695, Leibniz dichiarava a Bernoulli la possibilità di sviluppare una serie infinita mediante l’applicazione di un esponente frazionario a una base differenziale (d/dx)KF, così da “produrre una progressione geometrica, […] un’analogia meravigliosa”.[7]
Altrove, Leibniz fornisce una concezione teofanica e cosmologica della scalarità frattale: non solo è infinita la materia in perenne flusso in un mondo altrettanto infinito, ma sono infinite anche le anime e ciascuna “è uno specchio vivente perpetuo dell’universo”.[8] Ogni anima include l’intera serie del mondo che rispecchia dal proprio punto di vista, ogni punto di vista include oscuramente ogni altro. Sempre il filosofo tedesco, guardando per la prima volta nel microscopio progettato da Antonie van Leeuwenhoek (1632-1723) si meravigliò della qualità frattale degli organismi: “c’è un mondo di creature – di esseri viventi e di animali, di entelechie e di anime – anche nella più piccola porzione di materia”.[9]
Paolo Portoghesi (1931-2023) fu tra i primi a cogliere la profonda analogia tra le ricerche de Gli oggetti frattali e le architetture della sua amata Roma.[10]
A sua volta, Gilles Deleuze (1925-1995) ha avuto il merito di situare il Barocco a lato di Leibniz, in prossimità di Mandelbrot: l’architettura barocca si sviluppa passando “attraverso un numero infinito di punti angolosi, […] è la curva di Koch”.[11] Si pensi alle ipnotiche geometrie del Borromini (1599-1667) in Sant’Ivo alla Sapienza, alla cappella della Sacra Sindone del duomo di Torino progettata da padre Guarino Guarini (1624-1683) (Fig.2), all’utilizzo del bugnato con la sua qualità cavernosa.

Fig. 2
Possiamo andare ancora più in là, scorgere una qualità frattale nel radicale principio di pienezza di Giordano Bruno (1548-1600) o nei rapporti di autosimilarità astrologica che innervano le analogie micro e macro cosmiche dell’epoca rinascimentale.
Ancora, potremmo procedere a ritroso sino alle geometrie dell’architettura islamica,[12] come nei motivi decorativi dei “Muqarna” (مقرنص) (fig.3), oppure nel tempio di Brihadeshwara in India (fig.4).

Fig. 3
Fig. 4
Guardando alla storia dei giardini ritroviamo un doppia correlazione omotetica: è frattale la morfologia vegetale (le nervature delle foglie), ma qualcosa di frattale struttura le complesse razionalizzazioni arboree dell’orto botanico di Padova costruito nel 1545 (fig. 5),[13] oppure i giardini cinesi e giapponesi in cui la morfologia del paesaggio “in miniatura” dovrebbe rispecchiare il buon ordine del cosmo.[14]

Fig. 5
Cosa fare di tutta questa casistica? Imitazione della natura o sforzo descrittivo? Puro fatto artistico-espressivo? Cimeli di un passato incommensurabile?
Mandelbrot fu capace di sistematizzare sotto un unico nome un “museo degli orrori”[15]: la curva di Peano (fig.6) che passa per tutti i punti di un quadrato – paradosso di una superficie finita racchiusa da un perimetro infinito; la polvere di Cantor; le intuizioni di Jean Perrin che nel 1913 parlava di “curve senza tangente”.[16]
 Fig. 6
Fig. 6
Da allora la matematica frattale si è sviluppata in ogni direzione: nello studio delle fluttuazioni finanziare e nell’analisi dei dati biochimici, nella modellazione di fenomeni complessi e, non ultimo, nello sviluppo della Chaos theory a cui Henri Poincaré (1854-1912) diede un impulso fondamentale.
Dove collocare quel “reiterato abuso” dei concetti matematici a cui ci siamo precedentemente richiamati?
Si osservi ciò che scrivono Deleuze e Guattari in Mille piani (1980): l’interdimensionalità non è soltanto l’indicatore della dimensione non intera delle figure frattali, ma è anche segno di un divenire, di qualcosa che si muove tra i piani, una “zona di indiscernibilità propria del ‘divenire’”.[17] Un “tra” in cui la variazione prende vita: tutto ciò che è frattale sembra vivere e germogliare.
Parafrasando il matematico italiano Ernesto Cesaro (1859-1906), si potrebbe dire che la curva di Koch, se fosse viva, rinascerebbe in ogni punto dalle sue profondità.[18]
Le figure frattali hanno tuttavia un limite di scala, non vanno dall’infinitamente grande all’infinitamente piccolo: è una legge matematico-empirica che i due filosofi francesi sembrano violare apertamente.[19] È ciò che spinse Sokal e Bricmont ad affermare che la filosofia non aveva compreso il concetto.
Eppure, per un altro verso, Deleuze e Guattari ripropongono con un’espressione nuova le leggi imposte da Leibniz quasi tre secoli prima: l’anima è specchio dell’universo, ma si percepisce soltanto interamente come ininterrotta variazione metamorfica, rispecchiamento in perpetuo divenire dell’universo sin nelle sue più intime e infinite fibre.
É come l’esempio del movimento della mano proposto da Henri Bergson (1859-1941) ne L’evoluzione creatrice (1941): esternamente appare come figura (meccanicismo) o progetto (finalismo), ma a entrambe le visioni “manca l’essenziale: il divenire”.[20] Per Deleuze e Guattari è la rivendicazione di uno spazio dove al predominio della geometria euclidea si sostituisce l’imprevedibile variabilità della Natura, qualcosa di essenzialmente generativo. Pascal, navigando angosciosamente tra l’infinitamente grande e l’infinitamente piccolo, negava a sua volta le leggi imposte dalle vecchie corrispondenze simboliche micro e macro cosmiche a base di un solo infinito trascendente; Bruno contravveniva apertamente a una vecchia questio della scolastica secondo cui una creatura infinita era, per ciò stesso, contraddittoria.
———-
Dove arrestare questa violazione delle leggi determinate da ciascuna concettualizzazione?
C’è qualcosa di poetico, come scrive Franco Bifo Berardi: bisogna “far scivolare oltre il sistema stabilito dello scambio simbolico”.[21]
È proprio il filosofo italiano ad aver di recente risignificato la frattalità: segno sinistro – ma pur sempre segno – della frattalizzazione dei mercati e dello spazio pubblico (le bolle di cui si è tanto parlato non sono forse frattali?).
Riappare così l’ineliminabile figura di Leibniz: padre del contemporaneo panlogicismo metastabile e autovariante,[22] Berardi osserva che “gli individui sono frammenti di tempo precari, frattali uniformati dal processo di ricombinazione ininterrotta. […] il frattale automatizzato è il significato profondo dell’individualismo neoliberale”.[23]
Michel Serres (1930-2019), formatosi anch’egli su Leibniz, ha dato un nome a questo produttivo slittamento di principi, a questa non-regola dell’intromissione che sembra regnare anche nella storia della frattalità: parassitismo.[24]
Non dovrebbe sorprendere che anche il parassita sia frattale, è a un tempo parassitario e parassitato. Ed è sempre Michel Serres a chiedere: il parassita genera o corrompe il sistema?[25]
NOTE
[1] B. Mandelbrot, Gli oggetti frattali (1975), pp. 7-8. La curva di Kock è di dimensione=1,261859.
[2] B. Mandelbrot, The fractal geometry of nature, W. H. Freedman and company, San Francisco 1982, p. 404, p. 10.
[3] A. Sokal, J. Bricmont, Imposture intellettuali (1997), tr. it. F. Acerbi, M. Ugaglia, Garzanti, Milano 1999, p. 18.
[4] P. Portoghesi, Poesia della curva, Gangemi editore, Roma 2020, p. 61.
[5] B. Mandelbrot, Gli oggetti frattali, cit., pp. 21-44.
[6] B. Mandelbrot, The fractal geometry of nature, cit., p. 1.
[7] Ivi., p. 404.
[8] G. W. Leibniz, Monadologia (1720), tr. it. S. Cariati, Bompiani, Firenze 2017, p. 85, §56.
[9] Ivi, p. 89, §66.
[10] Si veda P. Portoghesi, Poesia della curva, cit., pp. 61-69.
[11] G. Deleuze, La piega (1988), tr. it. D. Tarizzo, Giulio Einaudi editore, Torino 1990, pp. 26-27. Per Irénée Scalbert anche l’arte gotica è contraddistinta da un principio di autosimilarità, si veda The nature of Gothic, AA Files, n. 72 (2016), pp. 73-77, 79-91, 93-95.
[12] P. Portoghesi, Poesia della curva, p. 62.
[13] Immagine tratta da L’invenzione del giardino occidentale, p. 56.
[14] Si veda P. Grimal, L’arte dei giardini (1974), Donzelli 2000, pp. 91-100.
[15] Mandelbrot, Gli oggetti frattali, cit., p. 01.
[16] Mandelbrot, 1977, The fractal geometry of nature, cit., p. 07.
[17] G. Deleuze, F. Guattari, Mille piani, p. 666. A p. 664,: “gli oggetti frattali” sono insiemi il cui numero di dimensioni è frazionario, non intero oppure intero, ma con variazione continua di direzione”. Mandelbrot scrive ne Gli oggetti frattali, p. 16, “là dove finora non si vedevano oche zone di transizione, […] io identifico delle zone frattali”.
[18] Si veda P. Portoghesi, Poesia della curva, cit., p. 64.
[19] Si veda B. Mandelbrot, The fractal geometry of nature, p. 783 e Gli oggetti frattali, pp. 21-44.
[20] H. Bergson, L’evoluzione creatrice, 1941, p. 81. Un esempio degno di nota è proposto da Tim Ingold in Siamo linee, p. 62, dove scrive che “il suolo, nella sua infinita varietà, ha una qualità frattale”.
[21] F. Bifo Berardi, Respirare, Luca Sossella editore, Roma 2019, p. 20.
[22] Ivi, p. 63.
[23] Ivi, p. 77.
[24] M. Serres, Il parassita (1980), a cura di G. Polizzi, Mimesis edizioni, Milano 2022.
[25] Ivi, p. 40.
BIBLIOGRAFIA
- Bergson, H., L’evoluzione creatrice (1941), tr. it. F. Polidori, Raffaello Cortina editore, Milano 2002.
- Bifo Berardi, F., Respirare, Luca Sossella editore, Roma 2019.
- Deleuze, G., Guattari, F., Mille piani (1980), tr. it. G. Passerone, Orthotes, Napoli-Salerno 2017.
- Deleuze, G., La piega (1988), tr. it. D. Tarizzo, Giulio Einaudi editore, Torino 1990
- Grimal, P., L’arte dei giardini (1974), tr. it. M. Magi, Donzelli editore, Roma, 2000.
- Ingold, T., Siamo linee (2015), it. D. Cavallini, Giovanni Treccani, Roma 2020
- Leibniz, G., W., Monadologia (1720), tr. it. S. Cariati, Bompiani, Firenze 2017.
- Mandelbrot, Benoît, “Is nature Fractal?”, Science, 1998, vol. 279, n. 5352, pp. 783-786.
- Mandelbrot, B., Gli oggetti frattali (1975), a cur di R. Pignoni, Giulio Einaudi editore, Torino 2000.
- Portoghesi, P., Poesia della curva, Gangemi editore, Roma 2020.
- Scalbert, I., The nature of Gothic, AA Files, n. 72 (2016), pp. 73-77, 79-91, 93-95.
- Serres, M., Il parassita (1980), a cura di G. Polizzi, Mimesis edizioni, Milano 2022.
- Sokal, , Bricmont, J., Imposture intellettuali (1997), tr. it. F. Acerbi, M. Ugaglia, Garzanti, Milano 1999.
- Vercelloni, M., Vercelloni, V., L’invenzione del giardino occidentale, Jaca Book, Firenze 2019.
Autore
-
Laureato Magistrale in Scienze Filosofiche all’Università degli Studi di Milano, costruisce dentro e fuori il pensiero filosofico. Logico, feroce, le sa tutte. Non lo cogli in fallo. Soprattutto sulla modernità.

